Kapitel IV - Von der Faulheit der Programmierer

Übersicht

Im Rahmen des Kapitels IV - Von der Faulheit der Programmierer - werden wir zwei in jeder Programmiersprache verfügbare Konstrukte kennenlernen, die uns die Arbeit im Rahmen der Programmierung weiter erleichtern. Es geht sogar noch einen Schritt weiter, wir werden sehen, dass uns diese beiden Konstrukte erst bestimmte Möglichkeiten bei der Programmierung eröffnen.
Die beiden Konstrukte sind

Variablen.
In Ansätzen haben wir diese schon im letzten Kapitel kennengelernt und genutzt. Wir werden den Einsatz und den Begriff in diesem Kapitel weiter vertiefen.
Schleifen.
Schleifen ermöglichen uns die leichte und flexible Wiederholung einzelner oder mehrerer Anweisungen. Durch den Einsatz von Schleifen können wir uns viel Arbeit bei der Programmierung sparen.

Lernziele
Am Ende dieses Kapitels kannst du

Variablen in deinen Programmen zielgerichtet einsetzen.
Regeln bei der Namenswahl von Variablen wiedergeben und einhalten.
Einsatzmöglichkeiten und Vorteile von Variablen erläutern.
den Begriff Kontrollstruktur erläutern.
die beiden grundlegenden Arten von Schleifen als Kontrollstruktur benennen.
Zählschleifen in deinen Programmen einsetzen.
die Begriffe Schleifenkörper und Schleifenkopf erläutern.
mittels der range()-Funktion schnell Tupel erzeugen, um diese in Zählschleifen zu verwenden.

Noch mehr Quadrate

Aufgabe 1

Unterschiedliche Quadrate, die von einem Turtle-Objekt gezeichnet wurden.

Ein Turtle-Objekt hat unterschiedliche Quadrate gezeichnet. Beschreibe den Unterschied zwischen den einzelnen Quadraten.

Lösung:
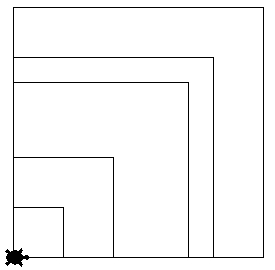
Die einzelnen Quadrate haben jeweils unterschiedliche Seitenlänge. Die Seitenlängen betragen 50, 100, 175, 200 und 250 Bildpunkte.

Aufgabe 2

Im letzten Kapitel haben wir ein Programm geschrieben, dass ein Quadrat zeichnet. Lade die zugehörige Datei wieder in PyScripter / Geany ("File / Datei -> Open").

Verändere das Programm so, dass es ein Quadrat mit der Seitenlänge 185 Bildpunkte zeichnet. Speichere das Programm unter einem passenden Dateinamen.
Verändere das Programm so, dass es ein Quadrat mit der Seitenlänge 90 Bildpunkte zeichnet. Speichere auch dieses Programm.
Erläutere, welche Veränderungen notwendig sind, um das Programm wie gewünscht anzupassen.

Lösung:

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines Quadrates mit 185 px Seitenlaenge 
from turtle import Turtle 
quadratTurtle = Turtle("turtle") 
quadratTurtle.forward(185) 
quadratTurtle.left(90) 
quadratTurtle.forward(185) 
quadratTurtle.left(90) 
quadratTurtle.forward(185) 
quadratTurtle.left(90) 
quadratTurtle.forward(185) 
quadratTurtle.left(90) 
# Fenster geoeffnet lassen - fuer Linux
quadratTurtle.screen._root.mainloop()

# Vollstaendiger Kopfkommentar s. oben 
# Zeichnen eines Quadrates mit 90 px Seitenlaenge 
from turtle import Turtle 
quadratTurtle = Turtle("turtle") 
quadratTurtle.forward(90) 
quadratTurtle.left(90) 
quadratTurtle.forward(90) 
quadratTurtle.left(90) 
quadratTurtle.forward(90) 
quadratTurtle.left(90) 
quadratTurtle.forward(90) 
quadratTurtle.left(90) 
# Fenster geoeffnet lassen - fuer Linux
quadratTurtle.screen._root.mainloop()

An den vier Programmstellen, an denen sich die Turtle jeweils vorwärts bewegt, müssen die Anzahl der Bildpunkte, also das Argument, entsprechend der Aufgabenstellung angepasst werden.

Wie du an der letzten Aufgabe gesehen hast, ist das entsprechende Suchen und Verändern der relevanten Stellen in diesem Fall vielleicht noch überschaubar, aber dennoch umständlich und fehleranfällig. Stellen wir uns nur vor, wir hätten einen Wert vergessen. Unter Umständen erinnerst du dich noch an die Möglichkeit, Wörter oder Zahlen zu suchen und zu ersetzen, die wir im Rahmen der Textverarbeitung kennengelernt haben. Diese Funktionalität stellt uns auch PyScripter zur Verfügung. Wir finden diese unter "Search -> Replace". Die meisten Programmierumgebungen haben diese Möglichkeit. Viele Programmierumgebungen haben noch mehr bzw. genauere Möglichkeiten zur Ersetzung.

Screenshot der "Suchen und Ersetzen" Möglichkeit von unserer Programmierumgebung "PyScripter"

Screenshot der "Suchen und Ersetzen" Möglichkeit von unserer Programmierumgebung "Geany"

Dadurch können wir uns sicherlich einen Teil der Arbeit ersparen. Optimal ist diese Lösung aber auch noch nicht: Angenommen, wir würden alle auftretenden Zahlen 90 durch die Zahlen 121 ersetzen wollen, wie in der obigen Abbildung dargestellt. Leider würde unser Programm danach kein Quadrat mehr zeichnen, da wir auch die Winkel, um die sich das Turtle-Objekt dreht, verändert haben. Ein ähnliches Problem hätten wir, wenn unser Programm zwei Quadrate zeichnet und wir nur eins davon verändern wollen.

Wir werden nun eine Möglichkeit kennenlernen, die Seitenlänge so in das Programm bzw. die einzelnen Anweisungen zu integrieren, dass eine einfache Veränderung möglich ist. Die zugehörige Technik haben wir schon im Zusammenhang mit der Namensgebung für Turtle-Objekte kennengelernt und wollen dieses jetzt etwas vertiefen bzw. ausbauen. Die zugehörigen Namen haben wir auch als Variablen bezeichnet, da sich die Objekte, auf die der Name zeigt, ändern können. (Das kannst du dir ungefähr so vorstellen, als wenn sich dein Lieblingsauto, -film oder -buch ändert: Der Name bzw. eigentlich die Bezeichnung (Lieblingsbuch o.ä.) bleibt gleich, aber das Objekt, dass du meinst, ist nun ein anderes.) Die Technik der Variablen wird in fast allen Programmiersprachen angeboten.

Noch mehr Variablen: "Namen" für Zahlen

Zur Erinnerung: Im letzten Kapitel haben wir durch die Anweisung

myTurtle = Turtle()

dem neu erstellten Turtle-Objekt den Namen myTurtle gegeben.

Abbildung: Sinngemäße Darstellung des
gespeicherten Turtle-Objektes

Abbildung: Ausschnitt des Speicherregales
mit den zugehörigen Beschriftungen

Durch die erfolgte "Namensgebung" konnten wir leicht auf das gespeicherte Objekt der Klasse Turtle zugreifen und seine Methoden aufrufen. Dabei ist es für uns unerheblich, an welcher Stelle im Speicher das Objekt genau gespeichert wurde. Den Speicher des Computers kann man sich als einen großen Schrank mit vielen Schubladen vorstellen. In jeder Schublade des Schrankes kann man etwas speichern oder ablegen. Zusätzlich kann man die Schubladen beschriften. Überträgt man die Vorstellung, so kann man sagen, dass die Schublade, in der sich unser neu erzeugtes Turtle-Objekt befindet (also gespeichert wurde) mit myTurtle beschriftet wurde. Wir hätten auch - wie bereits angesprochen - eine andere Beschriftung wählen können. Dabei muss bzw. sollte man nur zwei Sachen beachten:

Die entsprechende Beschriftung, die wir Name oder Variable genannt haben, muss die folgenden Regeln einhalten:
- Namen dürfen nur aus Buchstaben (ohne ä,ö,ü oder ß), Ziffern oder einem Unterstrich (_) bestehen. Das erste Zeichen darf allerdings KEINE Ziffer sein.
- Es dürfen einige reservierte Wörter nicht als Namen benutzt werden. Wir werden diese noch kennenlernen.
- Nach Möglichkeit soll der Name für ein Objekt mit einem Kleinbuchstaben beginnen.
Der Name sollte sinnvoll gewählt sein.
Stellen wir uns diesbezüglich einfach vor, dass wir bei sinnvoller Beschriftung der Schubladen schneller das gewünschte Objekt finden, als wenn wir einen anderen Namen wählen würden. Wer würde denn in einer Schublade, die mit "Schere" beschriftet ist, nach Süßigkeiten suchen?

Abmachung über Namen

Die Regel "Nach Möglichkeit soll der Name für ein Objekt mit einem Kleinbuchstaben beginnen." hat folgende Bewandtnis:
Namen von Klassen sollen stets mit einem Großbuchstaben beginnen. Hält man sich an die Vereinbarung und lässt Namen von Objekten immer mit einem Kleinbuchstaben beginnen, so kann man im Quellcode leicht zwischen Namen für Objekte und Klassen unterscheiden. Und du hast sicherlich schon gemerkt: Einfach zu lesender Quellcode ist die halbe Miete bei der Fehlersuche und -korrektur.

Wir haben bis jetzt nur die Klasse "Turtle" kennengelernt und mit zugehörigen Objekten gearbeitet. Streng betrachtet stimmt dies so nicht. In objektorientierten Programmiersprachen ist so gut wie alles ein Objekt. Wir haben zusätzlich bereits Zahlen (90, 180, 100, 200 etc.) und Zeichenketten ("Hallo Welt", "Fehler", "Das Ergebnis ist", "*" u. v. m.) kennengelernt und damit gearbeitet. Dabei handelt es sich ebenfalls um Objekte. Im Vergleich zu Objekten der Klasse "Turtle" oder anderen Klassen gibt es allerdings zwei (kleine) Unterschiede:

Bevor wir mit Objekten dieser Klassen arbeiten können, ist es nicht nötig, den zugehörigen Bauplan zu laden. Diese Baupläne werden automatisch geladen und sind verfügbar. Die automatische Bereitstellung liegt darin begründet, dass man Zeichenketten und Zahlen in quasi jedem Programm benötigt.
Die Erzeugung von Objekte der zugehörigen Klassen ist einfacher. Es genügt, 123 oder "Hallo" oder "Schulring 6" in einem Programm zu verwenden - die zugehörigen Objekte werden automatisch erstellt.

Einen weiteren Unterschied gibt es - bezogen auf unsere bisherige Arbeit mit Objekten der Klassen Zahl und Zeichenkette - noch, den wir jetzt betrachten und aufheben werden. Bisher haben wir noch keine Namen bzw. Variablen für Zahlen und Zeichenketten vergeben. Wir haben diese immer direkt verwendet, wenn wir sie gebraucht haben.

Aufgabe 3

Angenommen, du möchtest, dass die Variable / der Name umfang auf das Objekt 123 zeigt. Gib an, welche bekannte Anweisung dazu verwendet werden kann.

Lösung:

umfang = 123

Es handelt sich dabei um die bekannte Anweisung von der Zuweisung eines Namens zu einem Turtle-Objekt durch den Zuweisungsoperator. Diese setzt sich zusammen aus einem Namen, hier umfang, dem Zuweisungsoperator (=) und dem gewünschten Objekt, in diesem Fall 123.

Probieren wir es aus. Wir arbeiten vorerst einmal wieder innerhalb der Python-Shell, da wir hier einfach "Sachen" ausprobieren und testen können, ohne das wir jedes Mal ein ganzes Programm schreiben müssen.

umfang=123
umfang
123

Wir weisen der Variablen umfang den Wert bzw. das Objekt 123 zu. Ab sofort zeigt die Variable umfang auf das Objekt 123. Das erkennen wir an der anschließenden Abfrage der Variablen. Der Interpreter ersetzt die vorkommenden Variablen einer Anweisung vor der Ausführung durch den zugehörigen Wert. Es wird also zuerst umfang durch den zugehörigen Wert 123 ersetzt und anschließend ausgegeben.

Wie in der Mathematik können wir mit Variablen rechnen:

2*umfang
246

oder

umfang+umfang+umfang+umfang
492

Auch hier werden die Variablen wieder ersetzt, dann das Ergebnis berechnet und schließlich ausgegeben.

Wir können das Ergebnis einer Rechnung mit Variablen auch einer neuen Variablen zuweisen. Angenommen, die Variable umfang beschreibt den Umfang eines gleichseitigen Dreieckes. Dann kann man die Seitenlänge mit der folgenden Anweisung berechnen:

umfang/3
41.0

Dieses Ergebnis können wir nun einer weiteren Variablen zuweisen, beispielsweise seitenlaenge.

seitenlaenge=umfang/3
seitenlaenge
41.0

Ab diesem Zeitpunkt hat die Variable seitenlaenge den Wert 41,0. Auch hier gibt es wieder die folgende "Abarbeitungsreihenfolge":

Ersetze alle Variablen durch ihre Werte
Berechne das Ergebnis
Weise das Ergebnis der Variablen seitenlaenge zu

Nochmal zur Erinnerung: Wir müssen bei Dezimalzahlen uns an die englische Notation gewöhnen. Hier wird statt einem Komma ein Punkt als Dezimaltrennzeichen verwendet.

Mit der Anweisung

umfang = 17

können wir der Variablen nun einen neuen Wert bzw. ein neues / anderes Objekt zuweisen. Wie bereits im letzten Kapitel angesprochen rührt daher der Begriff Variable, weil das Objekt, auf das der Name zeigt oder verweist, wechseln kann, so wie oben geschehen. Die entsprechende Abfrage liefert nun:

umfang
17

Achtung: Eine Änderung dieser Variablen ändert keine andere Variable! Die Variable seitenlaenge hat immer noch ihren ursprünglichen Wert.

seitenlaenge
41.0

Dies liegt darin begründet, dass die Variable umfang bei der Berechnung des Wertes der Variablen seitenlaenge nur eine indirekte Rolle gespielt hat: Es wurde mit dem Wert / Objekt, auf das die Variable zeigt, gerechnet, nicht mit der Variablen an sich. Folglich ändert sich das Ergebnis der Rechnung im Nachhinein nicht.

Abbildung: Zuerst zeigt die Variable umfang auf
das Objekt 123

Abbildung: Nach einer Änderung zeigt die Variable umfang
auf das Objekt 17

Noch ein weiteres Beispiel: Möchten wir nun mit Hilfe der Variablen umfang, die den Umfang eines Quadrates angibt, den zugehörigen Flächeninhalt des Quadrates berechnen und in der Variablen flaecheninhalt speichern, so lautet die zugehörige Anweisung:

flaecheninhalt=(umfang/4)**2

Kannst du diese Anweisung sowohl mathematisch, als auch bezogen auf die Auswertung durch den Interpreter erklären? Wenn nicht, frage einen Mitschüler oder den Lehrer!

Aufgabe 4

In der Python-Shell werden die folgenden Anweisungen ausgeführt:

text="Hallo"
text2=text
text="Maus"
text1=text*3

Welche Ausgabe erwartest du bei den folgenden Eingaben:

```
text1
```
```
text2
```

Lösung:

```
'MausMausMaus'
```
```
'Hallo'
```

Hinweis: Die Zeichen " und ' sind in diesem Fall gleichbedeutend. Es handelt sich in beiden Fällen um Zeichenketten.

Aufgabe 5

In der Python-Shell werden die folgenden Anweisungen ausgeführt:

x="123"
x=x+"4"

Welche Ausgabe erwartest du bei der folgenden Eingabe:

Lösung:

'1234'

Zur Erklärung: Es handelt sich hier um Zeichenketten und nicht um Zahlen. Wir haben bereits in Kapitel 1 gesehen, dass man mit Zeichenketten nicht rechnen kann. Das Zeichen + hängt in diesem Fall die beiden Zeichenketten "123" und "4" einfach aneinander. Ähnlich zu der Anweisung "123"*3. Erkennst du eine Parallele zur Mathematik?
Dort kann man 12*3 als eine Kurzschreibweise für 12+12+12 deuten. Achte in Zukunft auf das unterschiedliche Verhalten des +-Zeichens, wenn dies in Zusammenhang mit Zahlen oder Zeichenketten auftritt.

Aufgabe 6

Es werden die Anweisungen

anrede="Hallo"
name="Maus"
grusszeile="Hallo Maus"

in der Python-Shell ausgeführt.
Gib eine weitere Anweisung an, die der Variablen grusszeile die obige Zeichenkette zuweist. Benutze dabei die beiden Variablen name und anrede.

Lösung:

grusszeile=anrede+" "+name

oder

grusszeile=anrede+" "
grusszeile=grusszeile+name

Es sind sicherlich noch weitere Lösungen möglich. Wenn du dir nicht sicher bist, ob deine Lösung richtig ist, probier es doch einfach aus!

Hinweise

Wir werden ab sofort nur noch die Bezeichnung Variable verwenden.
Wie du sicherlich bereits gemerkt hast, müssen Variablen nicht vorher angelegt oder durch sonstige Vorbereitungen "verfügbar" gemacht werden. Das ist in anderen Programmiersprachen unter Umständen anders. Die entsprechenden Programmiersprachen sind unter Umständen strenger und verlangen eine vorherige Festlegung aller Variablen. Bei einem Umstieg auf eine andere Programmiersprache kann diese Tatsache am Anfang oft gewöhnungsbedürftig sein.
Bevor wir mit einer Variablen rechnen oder arbeiten können, müssen wir ihr einen Wert bzw. ein Objekt zuweisen.
Eine Variable, die zuerst auf eine Zeichenkette zeigt, kann ohne Probleme später auf eine Zahl oder gar ein Turtle-Objekt zeigen bzw. verweisen. Auch dies ist nicht in allen Programmiersprachen möglich. Wie gesagt - andere Programmiersprachen sind da u. U. strenger.
Damit es nicht zu Verwechselungen und Problemen kommt, einigen wir uns darauf, dass wir vorerst eine Variable nur für ein einziges Objekt verwenden.

Nutzung von Variablen zum Zeichnen von "variablen" Quadraten

Doch nun zurück zu unserem ursprünglichen Problem: Wir wollen unser Programm insoweit variabler gestalten, als dass wir die gewünschte Seitenlänge des Quadrates nur an einer Stelle ändern müssen. Was verwenden wir dazu? - na klar - eine Variable. Welche Änderungen sind nun dazu nötig?

Bevor wir das erste Mal den Wert für unsere variable Seitenlänge verwenden wollen, müssen wir eine Variable anlegen, die auf den gewünschten Wert zeigt. Es bietet sich beispielsweise seitenlaenge als Variable an.
An allen Stellen, an denen wir die Seitenlänge benötigen, müssen wir statt der konkreten Seitenlänge die zugehörige Variable eintragen. Es wird dann mit dem Wert gearbeitet, der der Variablen zugewiesen wurde.

Aufgabe 7

Warum verwenden wir statt der Variablen seitenlaenge nicht die Variable Seitenlänge. Erläutere deine Antwort.

Lösung:
Eine Verwendung dieser Variablen ist nicht möglich. Dies hat einen Grund bzw. streng genommen sogar zwei Gründe:

Die Variable Seitenlänge enthält das Sonderzeichen ä. Daher ist eine entsprechende Verwendung als Variablenname nicht möglich.
Ferner hat man sich darauf geeignet, dass Variablennamen mit einem Kleinbuchstaben beginnen sollen. Dies hat u. a. den Grund, dass man der Meinung ist, dass entsprechende Quelltexte dann besser lesbar bzw. schneller zu überblicken sind.

Aufgabe 8

Öffne nochmals das Programm vom Anfang des Kapitels. Setze die gerade ausgeführten Änderungen um. Weise der Variablen den Wert 123 zu.

Lösung:

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines Quadrates mit der in der Variablen seitenlaenge gespeicherten Seitenlänge 
from turtle import Turtle 
quadratTurtle = Turtle("turtle") 
# Zuweisung des Wertes 123 zur Variablen seitenlaenge 
seitenlaenge = 123 
# Vorwärtsbewegung um den in seitenlaenge gespeicherten Wert 
quadratTurtle.forward(seitenlaenge) 
quadratTurtle.left(90) 
# siehe oben 
quadratTurtle.forward(seitenlaenge) 
quadratTurtle.left(90) 
quadratTurtle.forward(seitenlaenge) 
quadratTurtle.left(90) 
quadratTurtle.forward(seitenlaenge) 
quadratTurtle.left(90) 
# Fenster offen lassen - fuer Linux
quadratTurtle.screen._root.mainloop()

Wir haben unser Ziel erreicht: Wenn unser Programm nun auf einmal ein Quadrat mit einer anderen Seitenlänge zeichnen soll, so brauchen wir nur die Zeile

seitenlaenge = 123

zu ändern. An allen Stellen, an denen die gewünschte Seitenlänge benötigt wird, wird danach der "richtige" Wert benutzt.

Rechtecke mit variablen Seitenlängen

Aufgabe 9

Verändere das Programm aus der letzten Aufgabe so, dass aus dem Quadrat ein Rechteck wird: Die eine Seite soll doppelt so lang sein, wie die andere. In deinem Programm soll man nur die Länge der kürzeren Seite eingeben, die zweite Seite soll automatisch berechnet werden.
Speichere auch dieses Programm!

Lösung:
Eine mögliche Lösung sieht wie folgt aus.

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines Rechteckes mit der in der Variablen seitenlaenge gespeicherten Seitenlänge (bzw. der doppelten Länge)
from turtle import Turtle 
rechteckTurtle = Turtle("turtle") 
# Zuweisung des Wertes 123 zur Variablen seitenlaenge 
# hierbei handelt es sich um die kürzere Seitenlänge 
seitenlaenge = 123 
# Vorwärtsbewegung um den in seitenlaenge gespeicherten Wert 
rechteckTurtle.forward(seitenlaenge) 
rechteckTurtle.left(90) 
#  diese Seite muss doppelt so lang sein
rechteckTurtle.forward(2*seitenlaenge) 
rechteckTurtle.left(90) 
#  kurze Seite 
rechteckTurtle.forward(seitenlaenge) 
rechteckTurtle.left(90) 
#  diese Seite muss wieder doppelt so lang sein
rechteckTurtle.forward(2*seitenlaenge) 
rechteckTurtle.left(90) 
# Fenster offen lassen - fuer Linux
rechteckTurtle.screen._root.mainloop()

Alternativ kann man auch eine zweite Variable anlegen und dieser den doppelten Wert der ersten Variablen zuweisen.

Aufgabe 10

Nun soll die eine Seite um 100 Bildpunkte kürzer sein als die andere. Die Variable seitenlaenge soll dabei auf die Länge der längeren Seite verweisen.
Gibt es eine Einschränkung für die Werte der Variablen seitenlaenge?
Speichere auch dieses Programm! Achte auf einen sinnvollen Dateinamen.

Lösung:
Eine mögliche Lösung sieht wie folgt aus.

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines Rechteckeckes mit den Seitenlängen seitenlaenge bzw. seitenlaenge-100 
from turtle import Turtle 
rechteckTurtle = Turtle("turtle") 
# Zuweisung des Wertes 123 zur Variablen seitenlaenge 
# hierbei handelt es sich um die längere Seitenlänge 
seitenlaenge = 123 
# Vorwärtsbewegung um den in seitenlaenge gespeicherten Wert 
rechteckTurtle.forward(seitenlaenge) 
rechteckTurtle.left(90) 
#  diese Seite muss 100 Bildpunkte kürzer sein
rechteckTurtle.forward(seitenlaenge-100) 
rechteckTurtle.left(90) 
#  kurze Seite 
rechteckTurtle.forward(seitenlaenge) 
rechteckTurtle.left(90) 
#  diese Seite muss 100 Bildpunkte kürzer sein
rechteckTurtle.forward(seitenlaenge-100) 
rechteckTurtle.left(90) 
# Fenster offen lassen - fuer Linux
rechteckTurtle.screen._root.mainloop()

Der Wert, auf den die Variable seitenlaenge zeigt, muss mindestens 101 groß sein. In diesem Fall ist die eine Seite 1 und die andere 101 Bildpunkte lang. Wäre die zweite Länge kleiner als Null, würde die Turtle rückwärts laufen. Dennoch erhalten wir ein Rechteck - probiere es ruhig aus. Denke auch bei der eigentlichen Aufgabe daran, dass du deine Lösung einfach selber kontrollieren kannst.

Nun sollen die beiden Seitenlängen unseres Rechteckes variabel und insbesondere voneinander unabhängig sein.

Aufgabe 11

Erläutere, wie du die oben genannte Anforderung an unser Programm zum Zeichnen eines Rechteckes erreichen kannst.

Lösung:
Wir müssen nun beide Seitenlängen in einer eigenen Variablen speichern und an den entsprechenden Stellen die Turtle-Objekte jeweils um die richtige Länge vorwärtsbewegen. Dazu gibt man die Variable als Argument der Methode an.

Aufgabe 12

Setze deine Überlegungen nun in ein Programm um. Speichere dieses unter einem sinnvollen Namen.

Lösung:

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines Rechteckes mit den Seitenlängen seitenlaenge1 und seitenlaenge2 
from turtle import Turtle 
rechteckTurtle = Turtle("turtle") 
# Zuweisung des Wertes 123 zur Variablen seitenlaenge1 
# das ist die Länge der ersten Seite 
seitenlaenge1 = 123 
# Zuweisung des Wertes 23 zur Variablen seitenlaenge2 
# das ist die Länge der zweiten Seite 
seitenlaenge2 = 23 
# Vorwärtsbewegung um den in seitenlaenge1 gespeicherten Wert 
rechteckTurtle.forward(seitenlaenge1) 
rechteckTurtle.left(90) 
#  Vorwärtsbewegung um den in seitenlaenge2 gespeicherten Wert
rechteckTurtle.forward(seitenlaenge2) 
rechteckTurtle.left(90) 
#  Vorwärtsbewegung um den in seitenlaenge1 gespeicherten Wert 
rechteckTurtle.forward(seitenlaenge1) 
rechteckTurtle.left(90) 
#  Vorwärtsbewegung um den in seitenlaenge2 gespeicherten Wert
rechteckTurtle.forward(seitenlaenge2) 
rechteckTurtle.left(90) 
# Fenster offen lassen - fuer Linux
rechteckTurtle.screen._root.mainloop()

Zur Übung: Dreiecke mit variabler Seitenlänge

Aufgabe 13

Schreibe ein Programm, das ein gleichseitiges Dreieck zeichnet. Die Seitenlänge soll später an einer Stelle änderbar sein.

Lösung:

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines gleichseitigen Dreiecks mit der Seitenlänge seitenlaenge 
from turtle import Turtle 
dreieckTurtle = Turtle("turtle") 
# Zuweisung des Wertes 95 zur Variablen seitenlaenge 
# dies wird später die Seitenlänge des gleichseitigen Dreiecks 
seitenlaenge = 95 
# Vorwärtsbewegung um den in seitenlaenge1 gespeicherten Wert 
dreieckTurtle.forward(seitenlaenge) 
# Drehung um 120 Grad (inkl. Wiederholung einiger Anweisungen)
dreieckTurtle.left(120) 
dreieckTurtle.forward(seitenlaenge) 
dreieckTurtle.left(120) 
dreieckTurtle.forward(seitenlaenge) 
dreieckTurtle.left(120) 
# Fenster offen lassen - fuer Linux
dreieckTurtle.screen._root.mainloop()

Aufgabe 14

Gibt es einen weiteren Wert, den man in einer Variablen speichern könnte? Erkennst du an dieser zusätzlichen Variablen einen Vorteil?

Lösung:
Wir können zusätzlich den Winkel, um den das Turtle-Objekt sich drehen muss, in einer Variablen speichern.

# # Autor(en) 
# Christian Graf 
# # Datum 
# 06.03.2011 
# # letzte Aenderung 
# 06.03.2011 
# # Beschreibung 
# Zeichnen eines gleichseitigen Dreiecks mit der Seitenlänge seitenlaenge 
from turtle import Turtle 
dreieckTurtle = Turtle("turtle") 
# Zuweisung des Wertes 95 zur Variablen seitenlaenge 
# dies wird später die Seitenlänge des gleichseitigen Dreiecks 
seitenlaenge = 95 
# Speichern des Drehwinkels in einer zusätzlichen Variablen 
drehwinkel = 120 
# Vorwärtsbewegung um den in seitenlaenge1 gespeicherten Wert 
dreieckTurtle.forward(seitenlaenge) 
# Drehung um den entsprechenden Drehwinkel (in der Variablen drehwinkel) 
dreieckTurtle.left(drehwinkel) 
dreieckTurtle.forward(seitenlaenge) 
dreieckTurtle.left(drehwinkel) 
dreieckTurtle.forward(seitenlaenge) 
dreieckTurtle.left(drehwinkel) 
# Fenster offen lassen - fuer Linux
dreieckTurtle.screen._root.mainloop()

Diese Änderung mag vielleicht auf den ersten Blick keinerlei Vorteile oder Verbesserungen bringen. Möchte man aber beispielsweise dieses Programm als Grundlage verwenden, um ein Fünfeck zu zeichnen, so reicht es, die Anweisungen in den Zeile 20 und 21 zu kopieren und zweimal einzufügen. An diesen Zeilen müssten keine Änderungen durchgeführt werden. Lediglich der Winkel in der Variablen drehwinkel müsste geändert werden.
Mache dir an einer Skizze klar, warum der entsprechende Drehwinkel 72° groß ist. Solltest du Probleme haben, frage einen Mitschüler oder den Lehrer. Zur Übung kann es nicht schaden, wenn du das entsprechende Programm ebenfalls einmal schreibst bzw. dir aus der Vorlage "zusammenkopierst". Speichere auch dieses Programm unter einem sinnvollen Dateinamen.
Allgemein kann bzw. sollte man alle Werte, die mehrfach verwendet werden, in Variablen speichern. Bei Werten, die nur an einer Stelle verwendet werden, ist dies Geschmackssache.

Immer und immer wieder: Wiederholungen

Wie du sicherlich schon gemerkt hast, wiederholen sich beim Zeichnen eines Dreiecks, Vierecks, Fünfecks immer wieder die folgenden Anweisungen:

myTurtle.forward(seitenlaenge) 
myTurtle.left(drehwinkel)

Als Nächstes wollen wir die vorliegende Treppe hinsichtlich vorhandener Wiederholungen von Anweisungen untersuchen.

Zeichnung der Treppe für die nächste Aufgabe

Aufgabe 15

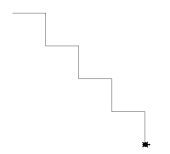
Überlege, in welche gleichartigen, sich wiederholenden Elemente sich die Treppe zerlegen lässt.
Aus wie vielen einzelnen Anweisungen setzt sich ein solches Element zusammen? Formuliere die Anweisungen in der Programmiersprache Python.

Lösung:

Die Treppe lässt sich in die einzelnen Treppenstufen zerlegen. Diese werden jeweils nacheinander gezeichnet.
Eine einzelne Stufe kann man mit 4 Anweisungen zeichnen.
```
treppenTurtle.forward(100)
treppenTurtle.right(90)
treppenTurtle.forward(100)
treppenTurtle.left(90)
```
Die gesamte Treppe zeichnet man, indem man diese Anweisungen viermal hintereinander ausführt.

Möchte man nun eine solche Treppe zeichnen, so kann man einerseits die Anweisungen entsprechend oft kopieren und in das Programm einfügen. Dies ist aber meistens mühselig, fehleranfällig und nervig. Ferner funktioniert diese Art der "Wiederholung von Anweisungen" nur, wenn wir im Vorfeld wissen, wie oft die Anweisungen wiederholt werden müssen. Dies ist beispielsweise nicht möglich, wenn der Benutzer zu Beginn des Programms gefragt werden soll, wie viele Stufen die Treppe haben soll.

Eingabefeld für die Anzahl der Treppenstufen

Daher muss eine andere Möglichkeit her, Wiederholungen oder die Anzahl der Wiederholungen auf einfache Weise in einem Programm umzusetzen. Die entsprechende Möglichkeit werden wir jetzt kennenlernen.

In allen Programmiersprachen gibt es die Möglichkeit, den Ablauf eines Programmes oder einzelner Programmteile zu steuern. Dies erfolgt mittels sogenannter Kontrollstrukturen. In dem hier vorliegenden Fall werden wir eine Kontrollstruktur benutzen, die die Wiederholungen einzelner oder mehrerer Anweisungen ermöglicht. Die Steuerung oder die Beeinflussung der Wiederholungen im Programmablauf erfolgt mittels sogenannter Schleifen. Schleifen sind ein mögliches Beispiel für Kontrollstrukturen. Wir werden im weiteren Verlauf des Leitprogrammes noch eine weitere Kontrollstruktur, sog. Verzweigungen, kennenlernen. Bisher wurde in unseren Programmen eine Zeile nach der anderen abgearbeitet. Durch den Einsatz von Schleifen wird dies nun geändert. Mittels Schleifen sind wir in der Lage, einzelne oder mehrere Zeilen mehrmals ausführen zu lassen.

Bei der Kontrollstruktur "Schleife" unterscheidet man zwischen zwei grundlegenden Arten:

Zählschleifen
Bei diesen Schleifen ist vorher festgelegt, wie oft eine oder mehrere Anweisungen wiederholt werden.
Bedingte Schleifen
Bei diesen Schleifen werden die zugehörigen Anweisungen solange wiederholt, wie eine bestimmte Bedingung erfüllt ist. Beispielsweise solange, wie der Benutzer die linke Maustaste drückt.

Wir wollen uns hier auf sog. Zählschleifen beschränken.

Aufgabe 16

Kopiere das folgende Programm in eine neue Datei. Speichere es unter dem Dateinamen "ErsteSchleife.py" und führe es aus.

# Christian Graf / 06.03.2011 / erste Schleife
for i in (0,1,2,3,4):
	print("Nächste Zahl:")
	print(i)

Welche Ausgabe erhältst du? Kannst du diese Ausgabe erklären?
Es ist wichtig, dass du die entsprechende Einrückung des Quellcodes mit übernimmst. Warum dies wichtig ist, werden wir gleich sehen.

Lösung:

Nächste Zahl:
0
Nächste Zahl:
1
Nächste Zahl:
2
Nächste Zahl:
3
Nächste Zahl:
4

Scheinbar werden die Anweisungen in den Zeilen 03 und 04 mehrfach ausgeführt. Offensichtlich wechselt dabei der Wert der Variablen i. Es fällt auf, dass genau die in Zeile 02 stehenden Werte dafür eingesetzt werden.

Aufgabe 17

Versuche das obige Programm so zu erweitern bzw. umzubauen, dass du die folgende Ausgabe erhältst.

0
Nächste Zahl: 1
Nächste Zahl: 2
Nächste Zahl: 3
Nächste Zahl: 4
Nächste Zahl: 5
Nächste Zahl: 6
Nächste Zahl: 7
Nächste Zahl: 8
Nächste Zahl: 9
Ende!

Lösung:

# Christian Graf / 06.03.2011 / erste Schleife
print(0)
for i in (1,2,3,4,5,6,7,8,9):
	print("Nächste Zahl: ",i)
print("Ende!")

Es gibt zwei Zeilen, die aus dem Muster herausfallen. Weiter wurden die zu wiederholenden Zeilen angepasst und der Wertevorrat in Zeile 02, jetzt in Zeile 03, erweitert. Probiere einmal aus, die Einrückung in Zeile 05 genau wie in Zeile 04 vorzunehmen - erkennst du einen Unterschied und damit die Bedeutung der Einrückung?

Die for-Schleife

Die sog. for-Schleife, die du gerade kennengelernt und bereits benutzt hast, zählt zu den sog. Zählschleifen. Sie besteht aus zwei wichtigen Teilen:

Schleifenkopf
In der zweiten Aufgabe war das
```
for i in (1,2,3,4,5,6,7,8,9):
```
und in der ersten Aufgabe
```
for i in (0,1,2,3,4):
```
Schleifenkörper
In der zweiten Aufgabe war das
```
	print("Nächste Zahl: ",i)
```
und in der ersten Aufgabe
```
	print("Nächste Zahl:")
	print(i)
```

Der Schleifenkörper umfasst alle Anweisungen, die wiederholt ausgeführt werden sollen. Du hast sicherlich schon bemerkt, dass diese eingerückt sind. Diese Einrückung erfolgt mittels der sog. Tabulatortaste. Du findest diese am linken Rand der Tastatur, aufgedruckt sind zwei entgegengesetzt ausgerichtete Pfeile. Da Informatiker aber faule Menschen sind, übernimmt die Programmierumgebung in vielen Fällen die Einrückung für uns. Wir müssen die Einrückung nur beenden, wenn wir nicht mehr wollen, dass eine Anweisung zum Schleifenkörper gehört und damit mehrmals ausgeführt werden soll. Beispiel:

# Hier steht der Schleifenkopf
	# auf diese Höhe stehen alle
	# Anweisungen, die zur Schleife gehören
	# hier auch noch
# Die Anweisungen ab hier werden nicht mehr wiederholt, sondern
# normal ausgeführt.

Versuche den Unterschied der Einrückung an dem folgenden kleinen Programm nochmals nachzuvollziehen.

for i in (1,2):
	print("Hallo")
print("Auf Wiedersehen!")

Was passiert, wenn du die dritte Zeile auch noch einrückst?
Was passiert, wenn du die Einrückung in der zweiten Zeile entfernst?
Was passiert, wenn du die Einrückung in der dritten Zeile wieder entfernst?
Was passiert, wenn du die Einrückung in der zweiten Zeile verdoppelst?

Hinweise

Die Einrückungen bzw. das korrekte Einrücken von einzelnen Zeilen bzw. einzelnen Anweisungen ist in Python besonders wichtig. Daran macht der Interpreter nachher die Struktur des Programmes fest, um zu wissen, welche Anweisung wozu gehört. Die Anweisungen, die unterhalb des Schleifenkopfes stehen, also entsprechend zu dieser Schleife gehören, bezeichnet man auch als Anweisungsblock oder kurz Block. Dieser Block erstreckt sich nur über die zur Schleife gehörenden Anweisungen - dazu aber später mehr.
Auch in anderen Fällen, wenn Anweisungen eingerückt werden müssen, um eine bestimmte Zugehörigkeit auszudrücken, werden diese ebenfalls als Block bezeichnet. Die Abgrenzung einzelner Blöcke und auch die Zuordnung von Anweisungen zu einem Block ist wichtig.

Der Schleifenkopf der for-Schleife

Der Aufbau eines Schleifenkopfes der for-Schleife erfolgt immer nach dem gleichen Prinzip: Zuerst kommt das Schlüsselwort for gefolgt von einem gültigen Variablennamen. Es folgt das Schlüsselwort in. Anschließend folgt ein sog. Tupel von Werten. Die einzelnen Werte stehen durch Kommata getrennt innerhalb von runden Klammern. Werte können beispielsweise Zahlen oder Zeichenketten sein. Der Kopf wird mit einem Doppelpunkt abgeschlossen. An diesem erkennt Python bzw. der Interpreter den notwendigen Beginn eines Anweisungsblockes. Ein weiteres Beispiel. Hier befinden sich in dem Tupel allerdings keine Zahlen, sondern Zeichenketten:

for name in ("Peter","Gustav","Otto"):
	print("Hallo",name,"!")
print("Ende der Schleife!")

Du erkennst die beiden Schlüsselwörter for und in . Die Variable trägt die Bezeichnung name. Das Tupel umfasst die drei Zeichenketten "Peter", "Gustav" und "Otto".

Zum Schleifenkörper gehört in diesem Fall die Zeile 02, die Zeile 03 hingegen nicht, da diese nicht entsprechend eingerückt ist.

Lesen kann man den Schleifenkopf wie folgt: "Für jeden Wert in dem Tupel führe die folgenden (eingerückten) Anweisungen aus."

Achtung: Der Aufbau eines Schleifenkopfes unterscheidet sich von Programmiersprache zu Programmiersprache.

Wie wird die Schleife nun vom Computer bzw. dem Interpreter abgearbeitet? Der Variablen, in diesem Fall name, wird der erste Wert aus dem Tupel zugewiesen. Anschließend werden die Anweisungen aus dem Schleifenkörper ausgeführt. Überall, wo die Variable verwendet wird, wird entsprechend der zugewiesene Wert benutzt. Entsprechend erhalten wir die erste Ausgabe. Da der Schleifenkörper nun einmal durchlaufen wurde, geht es in die nächste Runde. Der Variablen wird der nächste Wert aus dem Tupel zugewiesen und der Schleifenkörper für diese Belegung ausgeführt. Das ganze wiederholt sich solange, bis dass alle Werte einmal verarbeitet wurden. Anschließend geht es mit der nächsten Anweisung, die auf den Anweisungsblock folgt, weiter. In dem obigen Beispiel wäre das Zeile 03.

Aufgabe 18

Erstelle ein Programm, das die folgende Ausgabe erzeugt. Benutze dazu die for-Schleife.

"Auf Wiedersehen Otto !"
"Auf Wiedersehen Gustav !"
"Auf Wiedersehen Petra !"
"Auf Wiedersehen Peter !"
"Alle Personen wurden erfolgreich verabschiedet."

Lösung:

# Kopfkommentar nicht vergessen ;)
for person in ("Otto","Gustav","Petra","Peter"):
	print("Auf Wiedersehen",person,"!")
print("Alle Personen wurden erfolgreich verabschiedet.")

Aufgabe 19

Erstelle ein Programm, das das Quadrat der Zahlen 1 bis 10 ausgibt. Benutze dazu die for-Schleife.

Lösung:

# Kopfkommentar auch hier nicht vergessen ;)
for zahl in (1,2,3,4,5,6,7,8,9,10):
	print(zahl,"zum Quadrat macht",zahl**2)
print("Aufgabe erledigt!")

Man kann for-Schleifen auch schachteln, d.h. innerhalb einer for-Schleife wird eine weitere for-Schleife ausgeführt. Wenn man dies in einem Programm umsetzen möchte, muss man darauf achten, dass man den Schleifenkörper der zweiten Schleife weiter einrückt. Es wird also innerhalb des ersten Blockes ein zweiter, tiefer eingerückter Block eingerichtet.

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Ausgabe des kleinen 1x1
for zahl1 in (1,2,3,4,5,6,7,8,9,10):
	print("Die Zahlenreihe zur Zahl:",zahl1)
	for zahl2 in (1,2,3,4,5,6,7,8,9,10):
		print(zahl2,"*",zahl1,"=",zahl1*zahl2)
print("Auftrag erfolgreich beendet.")

Probiere das Programm ruhig aus. Du wirst feststellen, dass die Eingabe von vier Zeilen Quellcode reicht, um das Ergebnis von 100 Rechnungen auszugeben. All das geht mittels Schleifen. Wir legen einfach fest, was wiederholt werden soll (Schleifenkörper) und wie es wiederholt werden soll (Schleifenkopf).

Auch bei diesem Programm wollen wir uns noch einmal kurz darüber unterhalten, wie das Programm bzw. in welcher Reihenfolge und mit welchen Variablen die einzelnen Anweisungen ausgeführt werden.
Zuerst stellen wir fest, dass in den Schleifenköpfen zwei Variablen verwendet werden, zahl1 und zahl2. Zuerst wird der Variablen zahl1 der Wert 1 zugewiesen. Anschließend erfolgt die Ausgabe der Zeile "Die Zahlenreihe zur Zahl: 1". Nun beginnt die zweite Schleife. Der Variablen zahl2 wird der erste Wert des Tupel zugewiesen, also ebenfalls die 1. Danach wird "1 * 1 = 1" ausgegeben, vergleiche dazu Zeile 07.
Nun geht es weiter mit dem zweiten Wert aus dem Tupel im zweiten Schleifenkopf, da noch nicht alle Anweisungen der zweiten Schleife abgearbeitet wurden. Die Variable zahl2 bekommt nun den Wert 2, die Variable zahl1 bleibt unverändert. Es wird die Zeile "2 * 1 = 2" ausgeben. Die Variable zahl2 bekommt nun den Wert 3 zugewiesen. Erst wenn die Variable zahl2 den Wert 10 zugewiesen bekommen hat, und die entsprechende Ausgaben von "10 * 1 = 10" erfolgt ist, ist die innere Schleife (Zeile 06) beendet (abgearbeitet). Nun wird der Variablen zahl1 der zweite Wert, also 2, zugeordnet. Das Spiel wiederholt sich. Versuche die Ausführungen des zweiten Durchlaufes der ersten Schleife anhand der Programmausgabe nachzuvollziehen.

Quizfrage: Angenommen du möchtest, dass nach jeder Zahlenreihe ausgegeben wird, dass die Zahlenreihe beendet ist. Vor welcher Zeile musst du die entsprechende Ausgabe einfügen? Wie weit musst du diese einrücken? Wenn du eine Idee hat - probier's aus!

Reservierte Wörter

Du erinnerst dich sicherlich an die genannten Regeln für die Wahl von Variablen:

Variablen dürfen nur aus Buchstaben (ohne ä,ö,ü oder ß), Ziffern oder einem Unterstrich (_) bestehen. Das erste Zeichen darf allerdings KEINE Ziffer sein.
Es dürfen einige reservierte Wörter nicht als Variablen benutzt werden.
Nach Möglichkeit sollte die Variable für ein Objekt mit einem Kleinbuchstaben beginnen.

Wir kennen mittlerweile vier reservierte Wörter:

import
from
for
in

Wir dürfen diese nicht als Variablen verwenden. Das liegt daran, dass Python bei dem Schlüsselwort for den Beginn einer for-Schleife erwartet. Anweisungen, wie beispielsweise

for = 19

oder

import = Turtle()

würde Python nicht verstehen und ausführen. Der Interpreter meldet in diesem Fall einen Syntaxfehler, da er den Beginn einer for-Schleife oder einer Import-Anweisung erwartet, aber eine Wertzuweisung vorfindet. In diesem Fall wäre die Syntax der for-Schleife oder der Import-Anweisung nicht eingehalten. Diese würde aber von dem Interpreter in diesem Fall erwartet werden.

Zurück zu den Turtle-Objekten: Zeichnen per Schleife

Aufgabe 20

Erstelle ein Programm, das ein Dreieck mit einer Seitenlänge von 100 Bildpunkten erstellt. Benutze dazu die for-Schleife. Achte darauf, dass der Drehwinkel und die Seitenlänge einfach zu ändern bleiben.

Lösung:

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Zeichnen eines Dreieckes mittels einer Schleife
from turtle import Turtle
myTurtle = Turtle("turtle")
seitenlaenge=100
drehwinkel=120
# Die Anweisung muss dreimal wiederholt werden, daher muss das Tupel drei Werte beinhalten.
for i in (0,1,2):
	myTurtle.forward(seitenlaenge)
	myTurtle.left(drehwinkel)
# Fenster offen lassen - fuer Linux
myTurtle.screen._root.mainloop()

Die Anweisungen zum Zeichnen des Dreieckes müssen drei Mal wiederholt werden. Daher muss das Tupel im Kopf der for-Schleife drei Werte beinhalten. Da wir diese Werte - im Vergleich zu den vorherigen Aufgaben - aber nicht weiter innerhalb des Schleifenkopfes brauchen können wir beliebige Werte wählen. Wir "missbrauchen" diese Werte einfach, um eine dreifache Wiederholung der gewünschten Anweisungen zu erreichen. Wir hätten genauso gut

for i in ("Montag","Dienstag","Donnerstag"):

oder

for i in ("x","y","z"):

oder gar

for i in (1,1,1):

wählen können. Wichtig ist nur, dass in dem Tupel insgesamt drei (gleiche) Zahlen oder (gleiche) Zeichenketten stehen.

Anhand der möglichen Wertevorräte erkennt man bereits, dass die Schleife viel mächtiger ist, als eine reine Wiederholung von Anweisungen auszuführen.

Aufgabe 21

Welche Änderungen müssen an dem Programm an der letzten Aufgabe durchgeführt werden, wenn wir nun ein Fünfeck (Seitenlänge 123 Bildpunkte) zeichnen wollen?

Lösung:

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Zeichnung eines Fünfeckes
from turtle import Turtle
myTurtle = Turtle("turtle")
seitenlaenge=123
drehwinkel=72
# Die Anweisung muss fünfmal wiederholt werden, daher muss das Tupel fünf Werte beinhalten.
for i in (5,5,5,5,5):
	myTurtle.forward(seitenlaenge)
	myTurtle.left(drehwinkel)
# Fenster offen lassen - fuer Linux
myTurtle.screen._root.mainloop()

In diesem Fall müssen wir den Winkel und die Anzahl an Wiederholungen verändern. Solltest du Probleme bei der Bestimmung des Winkels haben, so fertige eine Skizze an und trage alle bekannten Winkel ein. Schließe mit diesen dann auf die noch unbekannten Winkel. So erhälst du schlußendlich den gewünschten Winkel.

Aufgabe 22

Erstelle ein Programm, das die eben vorgestellte Treppe mittels einer Schleife zeichnet. Sowohl die Stufenhöhe als auch die Stufenbreite sollen variabel, also einfach zu ändern sein. Die zu zeichnende Treppe soll 10 Stufen umfassen.

Lösung:

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Zeichnen einer Treppe
from turtle import Turtle
myTurtle = Turtle("turtle")
stufenhoehe=15
stufenbreite=10
drehwinkel=90
# Wiederholung der Anweisungen zur Treppenzeichnung:
for i in (0,1,2,3,4,6,7,8,9):
	myTurtle.forward(stufenbreite)
	myTurtle.right(drehwinkel)
	myTurtle.forward(stufenhoehe)
	myTurtle.left(drehwinkel)
# Fenster offen lassen - fuer Linux
myTurtle.screen._root.mainloop()

Du kannst dein Programm ganz einfach kontrollieren, indem du die Treppe zeichnen lässt. Genügt es, bei deinem Programm die Längenangaben an einer Stelle zu ändern? Hast du das Programm unter einem sinnvollen Dateinamen gespeichert?
Prüfe, ob du einen Kopfkommentar geschrieben hast und deine Variablen sinnvoll bezeichnet hast.

Wie du gerade bei der Treppenzeichnung gesehen hast, ist die entsprechende Programmierung schon deutlich einfacher als das wiederholte Kopieren und Einfügen. Allerdings gibt es immer noch zwei Nachteile an unserer bisherigen Vereinfachung:

Angenommen, unsere Treppe soll 26 Stufen haben. Der Kopf der Schleife würde dann möglicherweise wie folgt aussehen:
```
for i in (0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25):
```
Wir müssten mühsam 26 Zahlen oder ähnliches in unser Tupel eintippen.
Angenommen, der Benutzer soll beim Start nach der Anzahl der Treppenstufen gefragt werden. In diesem Fall könnten wir keinen Schleifenkopf angeben, da wir nicht wissen, ob wir die Zahlen 0 bis 10 oder 0 bis 100.000 aufschreiben müssten.

Erinnerst du dich an die Überschrift? "Von der Faulheit der Programmierer"
Auch für diese beiden Probleme gibt es eine Lösung. Statt

for i in (0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25):

können wir einfach schreiben

for i in range(26):

Was wurde geändert: Statt eines Tupels hinter dem reservierten Wort in haben wir einen Funktionsaufruf angegeben. Dies ist die range()-Funktion. Als Argument haben wir dieser die Zahl 26 übergeben. Die range()-Funktion erzeugt nun ein Tupel mit 26 Werten für uns und setzt es an der benötigten Stelle (hinter dem reservierten Wort in) ein. Wir brauchen nun nicht mehr alle benötigten Einträge selber anzulegen, sondern teilen einfach der range()-Funktion mit, wie viele Einträge wir gerne hätten. Gleichzeitig können wir damit auch den zweiten Nachteil ausräumen: Wir übergeben die vom Benutzer gewünschte Anzahl einfach als Argument an die range()-Funktion.

Aufgabe 23

Gibt es eine Möglichkeit zu schauen, welche Werte das Tupel enthält, das die range()-Funktion für uns anlegt?

Lösung:
Selbstverständlich geht das. Wir lassen uns einfach die einzelnen Einträge mittels einer for-Schleife ausgeben.

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Ausgabe des Inhaltes des von der range()-Funktion erzeugten Tupels
for unbekannt in range(5):
	print(unbekannt)

Scheinbar legt der Aufruf der Funktion range(5) ein Tupel mit den Einträgen 0,1,2,3,4 an. Es werden also von der 0 ausgehend soviele Zahlen (aufsteigend) eingefügt, bis dass soviele Zahlen in dem Tupel enthalten sind, wie im Funktionsargument festgelegt wurden. Ein häufiger Fehler in diesem Zusammenhang ist, dass man annimmt, dass der Wert 5 ebenfalls in dem erzeugten Tupel enthalten ist. Wie wir gerade gesehen haben, ist dies aber nicht der Fall.

Variable n-Ecke

Verschiedene Figuren mit gleicher Seitenlänge, aber unterschiedlicher Anzahl an Ecken.

Ziel des letzten Abschnittes des vorliegenden Kapitels wird es sein, unser Programm zum Zeichnen eines Dreieckes oder Quadrates so umzubauen bzw. zu erweitern, dass wir nur noch an einer Stelle (zu Beginn versteht sich) die Anzahl an Ecken und die Seitenlänge festlegen müssen. Den Rest soll das Programm für uns erledigen bzw. berechnen.

Bei einem Dreieck müssen die Anweisungen zum Zeichnen einer Seite drei Mal wiederholt werden. Bei einem Quadrat vier Mal und bei einem Fünfeck fünf mal. Soll unsere Figur also nachher n Ecken haben, müssen wir die Anweisungen n Mal wiederholen. Das war der einfache Teil. Die Überlegung, um welchen Winkel wir drehen müssen, ist etwas schwieriger. Damit beschäftigt sich die folgende Aufgabe. Auch hier nochmal der Hinweis auf das Anfertigen einer Skizze!

Aufgabe 24

Ergänze die folgende Tabelle. Eine Skizze, in der du die Winkel markierst, kann helfen.

Anzahl Ecken	3	4	5	6	8	9	10	...	n
Drehwinkel (nach links)	120°	90°						...

Lösung:

Anzahl Ecken	3	4	5	6	8	9	10	...	n
Drehwinkel (nach links)	120°=360°/3	90°=360°/4	72°=360°/5	60°=360°/6	45°=360°/8	40°=360°/9	36°=360°/10	...	360°/n

Nun die letzte Aufgabe dieses Kapitels:

Aufgabe 25

Schreibe ein Programm, das mithilfe dieser beiden Variablen

anzahlecken = 10
seitenlaenge = 50

eine entsprechende Figur mit der festgelegten Seitenlänge und Anzahl an Ecken hat. Arbeite innerhalb des Schleifenkopfes bzw. -körpers nur mit diesen beiden Variablen.

Lösung:

# # Autor(en): Christian Graf
# # Datum: 12.03.2011
# # Beschreibung: Zeichnung eines n-Ecks
from turtle import Turtle
myTurtle=Turtle("turtle")
anzahlecken = 10
seitenlaenge = 50
drehwinkel = 360/anzahlecken
for i in range(anzahlecken):
	myTurtle.forward(seitenlaenge)
	myTurtle.left(drehwinkel)
# Fenster offen lassen - fuer Linux
myTurtle.screen._root.mainloop()

In der hier vorgestellten Lösung wurde zusätzlich eine dritte Variable benutzt. Dieser wurde der benötigte Drehwinkel mittels einer Rechnung auf Basis der gewünschten Anzahl an Ecken zugewiesen.

Das Turtle-Objekt hat unterschiedliche n-Ecke gezeichnet.

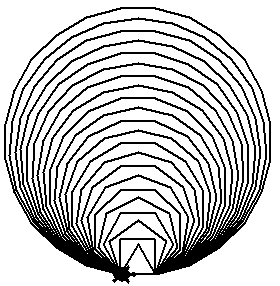
Damit sind wir nun in der Lage, uns mittels einer Schleife viel Programmierarbeit zu ersparen.

Durch die Kombination von zwei Schleifen kannst du beispielsweise das dargestellte Bild zeichnen. Die erste Schleife muss dazu allerdings eine andere Version der range()-Funktion benutzen. Diese hat, wie im Folgenden dargestellt, zwei Argumente:

for i in range(3,10):

Das erste Argument gibt die kleinste Zahl in unserem Tupel an. Bisher war das immer die null, in diesem Fall ist es die drei. Die höchste Zahl ist in diesem Fall die neun, also die Zahl vor dem zweiten Argument. Entsprechend umfasst

for i in range(1,4):

die Zahlen 1, 2 und 3. Probier's aus.

Falls es Probleme gibt oder du es nicht hinbekommst, kannst du das Programm hier herunterladen. Versuche es nachzuvollziehen. Ergänze ggf. einige Kommentare, so dass es dir später leichter fällt, das Programm nochmal nachzuvollziehen. Achte auf die Ausgabe in der Shell, diese kann dir dabei helfen.

Das Turtle-Objekt hat n-Ecke in unterschiedlichen Farben gezeichnet.

Im nächsten Kapitel werden wir eine weitere Kontrollstruktur kennenlernen, sog. Verzweigungen. Damit wird es uns möglich sein, beispielsweise jedes vierte n-Eck bei dem vorherigen Programm in rot, grün, blau oder gelb zu zeichnen. Ebenso gut können wir aber auch unser Programm aus der letzten Aufgabe so abändern, dass n-Ecke mit einer geraden Anzahl immer in grün gezeichnet werden und n-Ecke mit einer ungeraden Anzahl an Ecken in blau.

Mit der Kenntnis über diese beiden Kontrollstrukturen bist du dann bereits in der Lage, eine Vielzahl von unterschiedlichen Programmen (mittels eines Objektes der Klasse Turtle) zu schreiben.

Weiter geht's mit der Lernfortschrittskontrolle zu Kapitel IV.

zurück